KS Drift (Kolmogorov-Smirnov Test)

Key concept

A production set can be considered to have drifted with respect to a dataset if an important characteristic of the dataset is no longer present to the same extent in the production set or vice versa. In other words, the distributions computed on the dataset and the production set for at least one feature do not match anymore.

Computation

To detect if a drift has occurred, we perform a Kolgomorov Smirnov test which assumes that the empirical distribution functions for each feature extracted from the dataset and the production set are equal. We compute the test statistic D defined below:

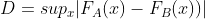
where Fa and Fb are the empirical distribution functions of the dataset and the production for one given feature
We reject the equality hypothesis at the alpha risk if the inequality below holds:

At the end of this test, we obtain a p-value after having fixed alpha (the probability of false alarm). The higher the p-value in front of alpha, the more we are sure to accept the hypothesis.

Interpretation

The p-value is inversely related to the maximum distance separating the two distribution functions. The greater the maximum distance, the more certain we are to reject the hypothesis, i.e. that the functions do not match.

The detection of a drift is to be monitored over the long term to define the type of drift: sudden, incremental/gradual or recurring/seasonal. Depending on the type of drift detected, either images from the production set must be added to the dataset or the model must be modified to accommodate the change.

Reference

Here is the research paper that inspired this metric 👉 Fast Unsupervised Online Drift Detection Using Incremental Kolmogorov-Smirnov Test